Answer:
a)
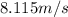
b)
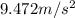
c)
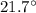
Step-by-step explanation:
The rest of the question is written below:
Determine (a) the bird’s speed relative to the ground; (b) the bird’s acceleration (magnitude and direction); and (c) the angle between the bird’s velocity vector and the horizontal.
And we have the following data:
 is the radius of the circular path in the x-axis
is the radius of the circular path in the x-axis
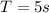 the period of the circular motion of the bird's path
the period of the circular motion of the bird's path
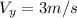 the vertical component of the bird's velocity, which is directed upward and is constant.
the vertical component of the bird's velocity, which is directed upward and is constant.
Now let's begin with the answers:
a) Bird’s speed relative to the ground
In order to find this speed, we have to calculate the magnitude of the bird's velocity vector:
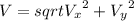 (1)
(1)
We already know the value of
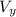 . So, we have to find
. So, we have to find
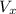 .
.
Since the bird is describing a circular path in the x-axis,
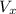 will be its tangential velocity:
will be its tangential velocity:
 (2)
(2)
Where
 is the birds angular velocity
is the birds angular velocity
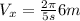 (3)
(3)
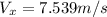 (4)
(4)
Substituting (4) in (1):
 (5)
(5)
 (6) This is the bird's speed relative to the ground
(6) This is the bird's speed relative to the ground
b) Bird’s acceleration (magnitude and direction)
Since the vertical component of the bird's velocity is constant, the vertical component of its acceleration is zero:

However, the bird has radial acceleration
 that results from its rotation on the circular path horizontally:
that results from its rotation on the circular path horizontally:
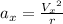 (7)
(7)
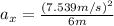 (8)
(8)
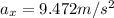 (9) This is the magnitude of the bird's acceleration, which is directed to the center of the circular path the bird describes while it is moving upwards in the spiral.
(9) This is the magnitude of the bird's acceleration, which is directed to the center of the circular path the bird describes while it is moving upwards in the spiral.
c) Angle between the bird’s velocity vector and the horizontal
In order to find the direction of the bird's velocity vector with the horizontal, we have to find the angle between the horizontal and the vertical component of this velocity:
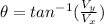 (10)
(10)
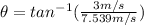 (11)
(11)
Finally:
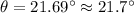 (12)
(12)