Question

The height of a triangle is 4 inches greater than twice its base. The area of the triangle is no more than 168 in.² which inequality can be used to find the possible lengths, x, of the base of the triangle?

A. x(x+2)=>168
B. x(x+2)=<168
C. 1/2x(x+4)=<168
D. 1/2x(x+4)=>168

Answer 1

Correct option: B

Explanation:

When we say a is no more than b, we express this in a mathematical language as follows:

`a\leq b`

In this inequality, we know that the area of the triangle is no more than 168 in². In other words, if the area is named
`A`, then:

`\mathbf{(1)} \ A\leq 168`

We also know that the height of a triangle is 4 inches greater than twice its base. Translating this in a mathematical language:

`\mathbf{(2)} \ h=2b+4 \\ \\ h:height \ of \ the \ triangle \\ \\ b:base \ of \ the \ triangle`

From geometry, we know that the area of a triangle is given by:

`\mathbf{(3)} \ A=(bh)/(2)`

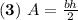
Matching (1), (2) and (3):

`(bh)/(2)\leq 168`

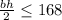
Since the length of the base of the triangle is
`x`, then
`b=x`

`(x(2x+4))/(2)\leq 168 \\ \\ Common \ factor \ 2: \\ \\ (2x(x+2))/(2)\leq 168 \\ \\ \boxed{x(x+2)\leq 168}`

Finally, correct option is B.