Answer:
a)
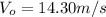
b)

Step-by-step explanation:
The complete question is written below:
An emu moving with constant acceleration covers the distance between two points that are 92 m apart in 6.5s. Its speed as it passes the second point is 14 m/s. What are (a) its speed at the first point and (b) its acceleration?
Since we are talking about constant acceleration, we can use the following equations:
 (1)
(1)
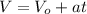 (2)
(2)
Where:
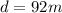 is the distance between the two points
is the distance between the two points
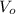 is the velocity of the emu at the first point
is the velocity of the emu at the first point
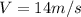 is the velocity of the emu at the second point
is the velocity of the emu at the second point
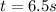 is the time it takes to the emu to cover the distance
is the time it takes to the emu to cover the distance

 is the emu's constant acceleration
is the emu's constant acceleration
Knowing this, let's begin with the answers:
a) Speed at the first point
In this situation wi will use equation (1):
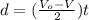 (1)
(1)
Finding
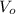 :
:
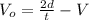 (3)
(3)
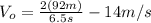 (4)
(4)
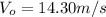 (5)
(5)
b) Emu's acceleration
Now we will substitute (5) in equation (2):
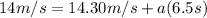 (6)
(6)
Finding
 :
:
 (7) This means the emu is decreasing its speed at a constant rate.
(7) This means the emu is decreasing its speed at a constant rate.