Question

What is the significance of the fact that the gravitational constant, G, is a very small number and that Coulomb’s constant, k, is a very large number?

The comparison indicates that the electromagnetic force is a much weaker force than the gravitational force.

>>>>>>>>>>>>>>>>The comparison indicates that the gravitational force is a much weaker force than the electromagnetic force.

The comparison does not give enough information to determine which force is weaker because the forces are in different units.

Answer 1

Answer: The comparison indicates that the gravitational force is a much weaker force than the electromagnetic force.

Explanation: Edge

Answer 2

The comparison indicates that the gravitational force is a much weaker force than the electromagnetic force. This is the significance of the fact that the gravitational constant, G, is a very small number and that Coulomb’s constant, k, is a very large number

Answer: The comparison indicates that the gravitational force is a much weaker force than the electromagnetic force.

Explanation:

We know that the universal formula for the estimation of gravitational force is,

`F=G *\left((m_(1) * m_(2))/(r^(2))\right)`

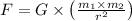
Where,

F, Gravitational force,
`m_(1) \text { and } m_(2)`- objects masses r- The relative distance between the two objects

G, Gravitational Constant
`6.67 * 10^(-11) (N m^(2))/(k g^(2))`

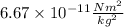
And, the electrostatic force between two scalar charges according to the Coulomb’s law is,

`F=k *\left((q_(1) * q_(2))/(r^(2))\right)`

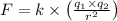
F, Electrostatic force between two charges,
`q_(1) \text { and } q_(2)`- Two scalar charges, r - The relative distance between two scalar charges, k- Coulomb’s constant
`8.987 * 10^(9) (N m^(2))/(c^(2))`

Now, on comparing the values of G and k, we can easily evaluate that eventually, the gravitational force will be lesser than the coulomb’s force.

Besides this, we can also judge this fact through various examples such as, a balloon rubbed with a cloth, easily sticks to the wall for some time. Opposing the gravitational force of the Earth which is not the case with the normal balloon.

It drops without having the electrostatic force between the wall and the balloon. This shows that the gravitational force draws lesser impact on objects as compared to the electrostatic force.