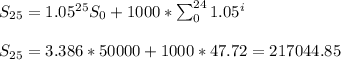Answer:
(a) The recurrence relation for the salary is
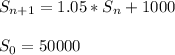
(b) The salary 25 years after 2017 will be $217044.85.
(c)

Explanation:
We can define the next year salary
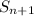 as
as
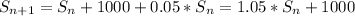
wit S0=$50000
If we extend this to 2 years from 2017 (n+2), we have

Extending to 3 years (n+3)
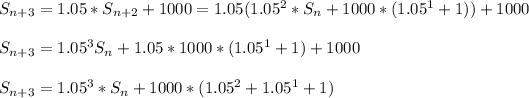
Extending to 4 years (n+4)
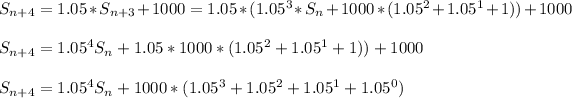
We can now express a general equation for S_n (salary at n years from 2017)

The salary at 25 years from 2017 (n=25) will be