Question

The commuting time for a student to travel from home to a college campus is normally distributed with a mean of 30 minutes and a standard deviation of 5 minutes. If the student leaves home at 8:25 A.M., what is the probability that the student will arrive at the college campus later than 9 A.M.?

Answer 1

0.1587

Explanation:

Let X be the commuting time for the student. We know that
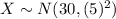`X\sim N(30, (5)^2)`. Then, the normal probability density function for the random variable X is given by

`f(x) = \frac{1}{\sqrt{2\pi(5)^(2)}}\exp[-((x-\mu)^(2))/(2(5)^(2))]`. We are seeking the probability P(X>35) because the student leaves home at 8:25 A.M., we want to know the probability that the student will arrive at the college campus later than 9 A.M. and between 8:25 A.M. and 9 A.M. there are 35 minutes of difference. So,

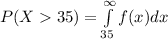`P(X>35) = \int\limits_(35)^(\infty)f(x)dx` = 0.1587

To find this probability you can use either a table from a book or a programming language. We have used the R statistical programming language an the instruction pnorm(35, mean = 30, sd = 5, lower.tail = F)