Answer:

Explanation:
The given compound inequality :
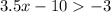 and
and

Consider ,
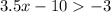
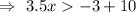 [Adding 10 both sides]
[Adding 10 both sides]

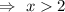 ...(i) [Dividing both sides by 2]
...(i) [Dividing both sides by 2]
Consider,

 [Add 9 both sides , we get]
[Add 9 both sides , we get]
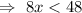
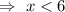 .....(ii)[Divide both sides by 8]
.....(ii)[Divide both sides by 8]
From (i) and (ii) , we have
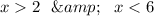
Thus , the solution is
 [values 2 and 6 are not included]
[values 2 and 6 are not included]