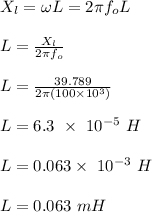Question

The current at resonance in a series L-C-R circuit is 0.2mA. If the applied voltage is 250mV at a frequency of 100 kHz and the circuit capacitance is 0.04 microfrad . Find the circuit resistance and inductance

Answer 1

• The resistance of the circuit is 1250 ohms

• The inductance of the circuit is 0.063 mH.

Step-by-step explanation:

Given;

current at resonance, I = 0.2 mA

applied voltage, V = 250 mV

resonance frequency, f₀ = 100 kHz

capacitance of the circuit, C = 0.04 μF

At resonance, capacitive reactance (
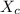`X_c`) is equal to inductive reactance (
`X_l`),

`Z = √(R^2 + (X_ l - X_c)^2) \\\\But \ X_l= X_c\\\\Z = R`

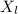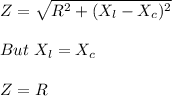
Where;

R is the resistance of the circuit, calculated as;

`R = (V)/(I) \\\\R = (250 \ * \ 10^(-3))/(0.2 \ * \ 10^(-3)) \\\\R = 1250 \ ohms`

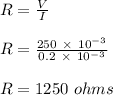
The inductive reactance is calculated as;

`X_l = X_c = (1)/(\omega C) = (1)/(2\pi f_o C) = (1)/(2\pi (100* 10^3)(0.04* 10^(-6) ) ) = 39.789 \ ohms\\`

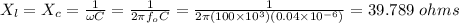
The inductance is calculated as;

`X_l = \omega L = 2\pi f_o L\\\\L = (X_l)/(2\pi f_o)\\\\L = (39.789)/(2\pi (100 * 10^3)) \\\\L= 6.3 \ * \ 10^(-5) \ H\\\\L = 0.063 * \ 10^(-3) \ H\\\\L = 0.063 \ mH`