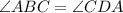Answer:
We used SSS rule of congruence to prove that the triangles are congruent.
Explanation:
We are given the following information in the question:
AB = CD
BC = DA
We have to prove that
We will first prove the congruency of triangle.
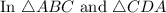
AB = CD ( Given )
BC = DA ( Given )
AC = CA (Common )
Hence,
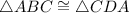 by SSS rule of congruence( Side Side Side).
by SSS rule of congruence( Side Side Side).
Since the triangles are congruent,