Question

A model rocket is launched in the air. The quadratic function is modeled by the equation y = - 16x ^ 2 + 32x where is measuring time and y is the height of the model rocket. What is the max height the rocket reaches?

Answer 1

The maximum height the rocket reaches is 16.

Explanation:

You know that a model rocket is launched in the air and the quadratic function is modeled by the equation y = -16*x² + 32*x where x is measuring time and y is the height of the model rocket.

A quadratic function or function of the second degree is a polynomial function defined by:

y= a*x² + b*x + c

A quadratic function has a maximum or a minimum and the vertex formula is used to get the highest or lowest value of the function. When a> 0, the vertex of the parabola is at the bottom of it, being a minimum (that is, the parabola opens "upward"), and when a <0 the vertex is at the top , being a maximum (that is, the parable opens "downward").

The value of the vertex on the x-axis can be calculated with the expression
`x=(-b)/(2*a)`

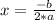
The value of the vertex on the y axis must be obtained by substituting the value of the vertex on the x axis in the function y= a*x² + b*x + c

In this case, a= -16, b=32 and c=0. Since a<0 the vertex will indicate the maximum of the function.

The value of the vertex on the x-axis is
`x=(-32)/(2*(-16))=1`

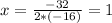
The value of the vertex on the y axis is:

y = -16*1² + 32*1

Solving:

y= -16*1 +32

y= -16 +32

y=16

The maximum height the rocket reaches is 16.