Answer:
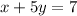
Explanation:
Point A
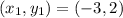
Point B
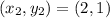
Now, slope of line passing through points (-3, 2) and (2, 1) :
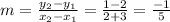
Now equation of line having slope-intercept form where slope is m and c is y intercept, is y = mx + c,
By substituting the value of m in above equation,
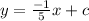
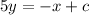 ...... (1)
...... (1)
Now since the line is passing through point (-3,2),therefore by substituting the value of x = -3 and y = 2 in above equation
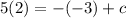
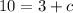

Now by substituting the value of c in eq (1)
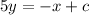
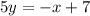
On rearranging the above expression,
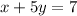
Therefore option (4) is the correct answer.