Question

Ezra works two summer jobs to save for a laptop that costs at least $1100. He decides to adjust his rates to $250 per lawn (x) for the summer and $300 per dog (y) for the summer, and to limit himself to 2 dogs. Describe how to find a solution graphically.

Answer 1

See explanation

Explanation:

Let x be he number of lawns and y be the number of dogs.

Ezra decides to adjust his rates

• to $250 per lawn, then for x lawns he has $250x;
• to $300 per dog, then $300y for y dogs.

The total cost is
`\$250x+\$300y`

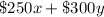
Ezra works two summer jobs to save for a laptop that costs at least $1100, so

`250x+300y\ge 1,100.`

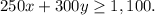
He has limit to 2 dogs, then
`y\le 2.`

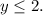
You get a system of two inequalities:

`\left\{\begin{array}{l}250x+300y\ge 1,100\\ \\y\le 2\end{array}\right.`

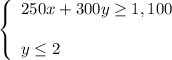
Plot the solutions sets on the coordinate plane (see attached diagram).

The common region (intersection of red and blue regions) is the solution set to the system of two inequalities.

So,

if y=2, then
`x\ge 2`

if y=1, then
`x\ge 3.2`

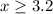
if y=0, then
`x\ge 4.4`

Answer 2

Which inequality represents this situation?

• 
  `250x + 300y \geqslant 1100`

1. If Ezra limits himself to 1 dog, how many lawns does he have to care for to reach his goal? - more than 3
2. What is a solution to the inequality? - (4, 1)
3. Describe how to find a solution graphically.

- Graph in the first quadrant because x and y are nonnegative. Determine and graph the inequality that represents the situation 250x + 300y >=1100. Shade the half-plane that does not include the origin since (0, 0) does not satisfy the inequality. Draw a horizontal line at Y = 2 for two dogs. Solutions lie on or below the part of the horizontal line that is in the shaded region.

(these answers were on e2020)