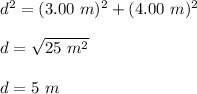Question

A cart travels 3.00 meters East and then 4.00 north. The magnitude of the carts resultant displacement is meters?

Answer 1

Answer:
`5\ meters`

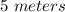
Step-by-step explanation:

Let be "d" the magnitude of the cart's resultant displacement in meters.

According to the information given in the exercise, the cart travels 3.00 meters East and then 4.00 North. Then, we get a right triangle (Observe the figure attached) where the hypotenuse "d" is the magnitude of the cart's resultant displacement.

In order to calculate "d", we need to use the Pythagorean Theorem:

`a^2=b^2+c^2`

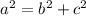
Where "a" is the hypotenuse, and "b" and "c" are the legs of the triangle.

In this case, we can identify that:

`a=d\\\\b=3.00\ m\\\\c=4.00\ m`

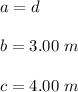
Then, substituting values and solving for "d", we get:

`d^2=(3.00\ m)^2+(4.00\ m)^2\\\\d=√(25\ m^2)\\\\d=5\ m`