Answer:
The total number of the payments is 18 ⇒ answer A
Explanation:
* Lets revise the rule of compounded monthly payment
→
![EMI=((A)(r))/([1-(1)/((1+r)^(n))])](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ycjpxpiokl7c6zsgp3y5aj1tu9grqxasxs.png) , where
, where
- A is the loan amount
- r is monthly interest in decimal (R/12*100))
- n the total number of payments
∵ A = $1100
∵ EMI = $71.5
- Interest rate is 19.2% APR
∵ r =

- Substitute these values in the rule to find n
∴ 71.5 =
![(1100(0.016))/([1-(1)/((1+0.016)^(n))])=(17.6)/([1-(1)/((1.016)^(n))])](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ry5tzkuax0oe88fsjhs6ov2flcqi90m0dn.png)
- By using cross multiplication
∴ 71.5[1 -
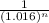 ] = 17.6
] = 17.6
- Divide both sides by 71.5
∴ 1 -
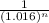 =
=

- Subtract 1 from both sides
∴ -
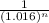 = -
= -
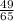
- Multiply both sides by -1
∴
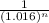 =
=
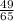
- By using cross multiplication
∴ 49[
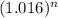 ] = 65
] = 65
- Divide both sides by 49
∴
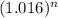 =
=
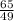
- Insert log for both sides
∴ ㏒
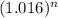 = log(
= log(
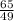 )
)
- Put n in-front of the ㏒
∴ n㏒(1.016) = ㏒(
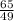 )
)
- Divide both sides by ㏒(1.016)
∴ n = 17.8 ≅ 18
* The total number of the payments is 18