Question

PLEASE HELP!

Determine between which consecutive integers the real zeros of f(x)=x^3-3x^2-2x+4 are located.

a.
between −2 & −1, between 3 & 4, and exactly at 1

b.
between −2 & −1, between 3 & 4, and exactly at –1

c.
between −1 & 0, between 3 & 4, and exactly at 1

d.
between −2 & −1, between 1 & 2, and exactly at 1

Answer 1

Answer a. between −2 & −1, between 3 & 4, and exactly at 1

Explanation:

In order to guide your reasoning and analysis, start by evaluating the function at the points they are suggesting in the answers: -2, -1, 0, 1, 3, and 4.

`f(x) = x^3 -3x^2-2x+4\\f(-2)= (-2)^3 -3 (-2)^2-2(-2)+4= -12\\f(-1)= (-1)^3 -3 (-1)^2-2(-1)+4= 2\\f(0)= (0)^3 -3 (0)^2-2(0)+4= 4\\f(1)= (1)^3 -3 (1)^2-2(1)+4= 0\\f(3)= (3)^3 -3 (3)^2-2(3)+4= -2\\f(4)= (4)^3 -3 (4)^2-2(4)+4= 12`

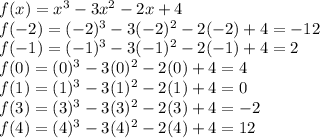
Therefore, since this is a polynomial function, and all polynomial functions are continuous, we can infer that when the function goes from a negative value to a positive value at a near by point, its graph must be crossing the x-axis and therefore adopting the value zero at that crossing.

From the particular x-values at which we evaluated this function, we notide:

1) We have one of the zero values of the function at x=1 because f(1) is zero.

2) at x=-2, f(-2) gives a negative value. But when evaluated at x=-1, f(-1) renders a positive value. Therefore there must be a crossing of the x-axis (and therefore a zero) in between these two numbers.

3) At x=-1, f(-1) equals 2 (not zero)

4) For x-values in between -1 and 0, we cannot say anything, because both render positive values for f(x).

5) For x=3 f(3) renders a negative value, and at x=4 f(4) gives a positive value. Therefore we know that in between those values of x, the graph must be crossing the x-axis, rendering a zero for the function.

From all the study above, we conclude that answer a. is the correct one.