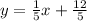Question

On a coordinate plane, a line goes through (negative 5, negative 4) and (0, negative 3). A point is at (negative 2, 2). What is the equation of the line that is parallel to the given line and passes through the point (–2, 2)? y = One-fifthx + 4 y = One-fifthx + Twelve-fifths y = –5x + 4 y = –5x + Twelve-fifths

Answer 1

(B) y=1/5x +12/5

Explanation:

Answer 2

Second option:
`y=(1)/(5)x+(12)/(5)`

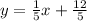
Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

We know that a line goes through the points
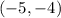`(-5,-4)` and
`(0,-3)`

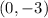
Since the line intersects the y-axis when
`x=0`, then the y-intercept of this line is:

`b=-3`

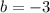
Substitute the y-intercept and coordinates of the point
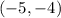`(-5,-4)` into the equation
`y=mx+b` and solve for "m":

`-4=m(-5)-3\\\\-4+3=-5m\\\\m=(-1)/(-5)\\\\m=(1)/(5)`

By definition, the slopes of parallel lines are equal, then the slope of the other line is:

`m=(1)/(5)`

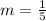
Knowing that it passes through the point
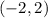`(-2, 2)`, we can substitute values into the equation
`y=mx+b` and solve for "b":

`2=(1)/(5)(-2)+b\\\\2+(2)/(5)=b\\\\b=(12)/(5)`

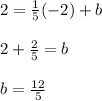
Therefoe, the equation of this line is:

`y=(1)/(5)x+(12)/(5)`