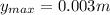Question

15. A football is kicked from the ground with an initial velocity of 25m/s at an angle of 28

degrees from horizontal.
a. Calculate the horizontal distance the football will travel in meters?
b. What is the maximum height during the football will achieve in meters during this kick?

Answer 1

Answers:

a) 52.87 m

b) 0.003 m

Step-by-step explanation:

This described situation is related to projectile motion and the equations that will be useful in this case are:

x-component:

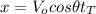`x=V_(o)cos\theta t_(T)` (1)

Where:

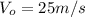`V_(o)=25m/s` is the football's initial speed

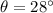`\theta=28\°` is the angle

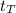`t_(T)` is the time since the football is kicked until it hits the ground

y-component:

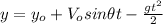`y=y_(o)+V_(o)sin\theta t-(gt^(2))/(2)` (2)

Where:

`y_(o)=0 m` is the initial height of the football (because is kicked from the ground)

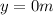`y=0 m` is the final height of the football (when it finally hits the ground)

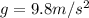`g=9.8m/s^(2)` is the acceleration due gravity

Knowing this, let's begin with the answers:

a) Horizontal distance

Firstly we need to calculate the total time the whole parabolic motion takes and this will be called
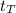`t_(T)`. From (2):

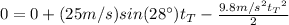`0=0+(25 m/s)sin(28\°) t_(T)-\frac{9.8m/s^(2){t_(T)}^(2)}{2}` (3)

Clearing
`t_(T)`:

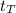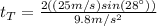`t_(T)=(2((25 m/s)sin(28\°)))/(9.8m/s^(2))` (4)

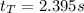`t_(T)=2.395 s` (5)

Now we can calculate the horizontal distance with this calculated time. Substituting (5) in (1):

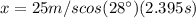`x=25 m/s cos(28\°)(2.395 s)` (6)

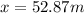`x=52.87 m` (7)

b) maximum height

The maximum height
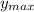`y_(max)` of the ball is reached when
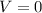`V=0` just at the middle of the parabolic motion, when the ball has been in air for half the time (
`t=(t_(T))/(2)=1.197s`).

Applying these conditions in (2):

`y_(max)=0+V_(o)sin\theta t-(gt^(2))/(2)` (8)

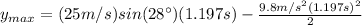`y_(max)=(25 m/s)sin(28\°)(1.197s)-(9.8m/s^(2)(1.197 s)^(2))/(2)` (9)

Finally:

`y_(max)=0.003 m`