Question

From the top of a cliff 92.9 m above a stream the angle of depression to a point on the near shore is 48.5 degrees and to a point on the far shore is 37.9 degrees find the width of the stream between these two points

Answer 1

37,15m

Explanation:

the distance between top of the cliff to the ground at shore level

and the distance between the top of the clif to the stream shore

defines a triangle rectangle.

Where:
`Tan(\alpha )=(opossite  side)/(adjacent side)=(x)/(y)  \\`

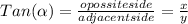
x= distance from shore to bottom of the cliff

y= distance from top of the cliff to the bottom of the cliff

`y*tan(\alpha)=x\\`

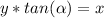
α1= 90°-48,5°= 41,5°

α2=90°-37,9°= 52,1°

x1= distance between near shore to the bottom of the cliff

x2= distance between far shore to the bottom of the cliff

`x1=y*tan(\alpha1)=92,9m*tan(41,5°) \\`

`x2=92,9m*tan(52,1°)`

`x2-x1=y*tan(\alpha2)-y*tan(\alpha1)`

`x2-x1=119,34°-82,19°`

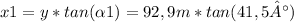
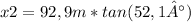
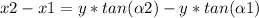
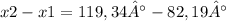
distance= 37,15°