Question

For the equation y= x2+2 x2−1 , express x in terms of y and determine the values of y for which x is real.

Answer 1

`x=\pm \sqrt{(y+2)/(y-1)}`

y can take on values in:

`(-\infty,-2] \cup (1,\infty)`

Explanation:

Hopefully this is the right equation:

`y=(x^2+2)/(x^2-1)`.

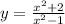Multiply both sides by
`x^2-1`:

`y(x^2-1)=(x^2+2)/(x^2-1)(x^2-1)`

`y(x^2-1)=x^2+2`

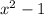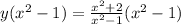
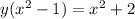
Distribute:

`yx^2-y=x^2+2`

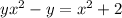
Put x terms on one side together and non-x terms on opposite side.

Add y on both sides

and subtract x^2 on both sides:

`yx^2-x^2=y+2`

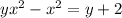
Factor:

`x^2(y-1)=y+2`

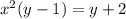
Divide both sides by (y-1):

`x^2=(y+2)/(y-1)`

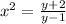
Now square root both sides:

`x=\pm \sqrt{(y+2)/(y-1)}`

y cannot be 1 because we don't want to divide by 0.

Now we also need to find when (y+2)/(y-1) is positive or zero because we can't square root negative values if we intend to have just real solutions.

The fraction is zero when y=-2 because that will give us 0 on top.

I'm going to draw a number line and test which intervals gives us positive values for our expression under the square root.

--------(-2)-------(1)----------

Plugging in -3 gives us (-3+2)/(-3-1)=(-1)/(-4)=1/4 so anything before -2 works.

Let's try 0: (0+2)/(0-1)=-2 so nothing between -2 and 1 will work.

Let's try it for 2: (2+2)/(2-1)=4/1=4 so anything after 1 will work.

So y can take on values in:

`(-\infty,-2] \cup (1,\infty)`