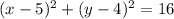Answer:
Explanation:
Given that a circle has tangents x=1, x=9 and y=0
Since two parallel lines are tangents the distance between these two lines give diameter of the circle
Distance between x=1 and x=9 is
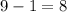 units
units
radius = 4 units ...i
Since y=0 is tangent, the centre will be having y coordinate as 4.
Since centre lies in the middle of x=1 and x=9 the centre will have x coordinate
as 5
Hence equation of the circle is