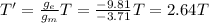Question

En la Tierra un volcán puede expulsar rocas verticalmente hasta una altura máxima H. A) ¿A qué altura (en términos de H) llegarían es- tas rocas si un volcán en Marte las expulsara con la misma velocidad inicial? La aceleración debida a la gravedad en Marte es de 3.71 m>s2, y se puede despreciar la resistencia del aire en ambos planetas. B) Si en la Tierra las rocas están en el aire un tiempo T, ¿por cuánto tiempo (en términos de T) estarán en el aire en Marte?

Answer 1

A) 2.64 H

The maximum height that the expelled rock can reach can be found by using the equation:

`v^2-u^2 = 2gd`

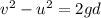
where

v = 0 is the velocity at the maximum height

u is the initial velocity

g is the acceleration of gravity

d is the maximum height

Solving for d,

`d=(-u^2)/(2g)`

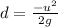
We see that the maximum heigth is inversely proportional to g. On the Earth,

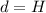`d=H` and
`g=g_e = -9.81 m/s^2`

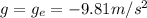
So we can write:

`(H)/(H')=(g_m)/(g_e)`

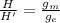
where H' is the maximum height reached on Mars, and
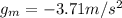`g_m = -3.71 m/s^2` is the acceleration of gravity on Mars. Solving for H',

`H' = (g_e)/(g_m)H = (-9.81)/(3.71)H=2.64 H`

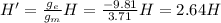
B) 2.64T

The time after which the rock reaches the maximum height can be found by using

`v=u+gt`

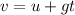
where

v = 0 is the velocity at the maximum height

u is the initial velocity

Solving for t,

`t=(v-u)/(g)`

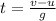
The total time of the motion is twice this value, so:

`t=2(v-u)/(g)`

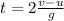
So we see that it is inversely proportional to g.

On the Earth, t = T. So we can write:

`(T)/(T')=(g_m)/(g_E)`

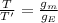
where T' is the total time of the motion on Mars. Solving for T',

`T' = (g_e)/(g_m)T=(-9.81)/(-3.71)T=2.64T`