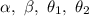Answer:
See explanation
Explanation:
Consider the first triangle:
1. From the right triangle with acute angle
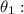
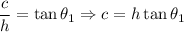
2. From the right triangle with acute angle
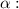
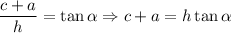
Thus,
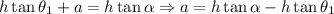
Consider the second triangle:
1. From the right triangle with acute angle
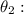
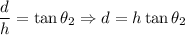
2. From the right triangle with acute angle
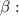
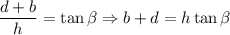
Thus,
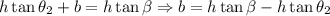
Now, since
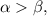 we have
we have
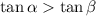 and
and

If
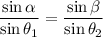
and
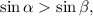
then
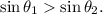
This means
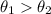 and
and
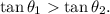
Hence,
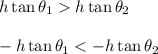
Now,
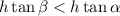
and
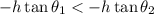
so
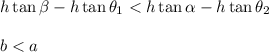
Note that this solution is true only for acute angles