The product of the roots of the equation : 1/2 x 2 - 5/4 x - 3=0

Question

asked Jul 18, 2020 208k views

2 Answers

Walter Luszczyk · Answer 1 · 2020-07-22T21:50:33+0000

Answer:

Product of the roots of the equation
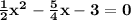$\bold{(1)/(2) x^(2)-(5)/(4) x-3=0}$ is -6

Solution:

If
$\alpha$ and
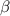$\beta$ are the roots of any quadratic equation
x^(2)+b x+c=0 then,

Sum of roots
$\alpha+\beta=-(b)/(a)$

Product of roots
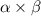$\alpha * \beta$ =
(c)/(a)

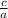
Given that

(1)/(2) x^(2)-(5)/(4) x-3=0

On simplifying the above equation,

(2 x^(2)-5 x-12)/(4)=0

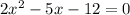
2 x^(2)-5 x-12=0

Here a = 2, b = -5 and c = -12

So product of roots is
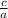(c)/(a) that is
(-12)/(2) = -6

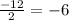
Hence product of the roots of the equation
(1)/(2) x^(2)-(5)/(4) x-3=0 is -6