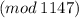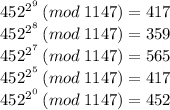Answer:
The answer is
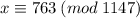
Explanation:
The following steps will give a solution to the congruence
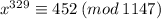
1. Compute Euler's Phi function
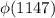 .
.
We have
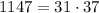 by prime factorization, so that
by prime factorization, so that
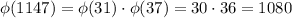
because
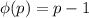 where p is a prime number.
where p is a prime number.
2. Find positive integers u and v that satisfy
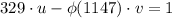 .
.
We know a solution exists, since
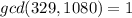 , using the Euclidean algorithm allows us to find the solution
, using the Euclidean algorithm allows us to find the solution
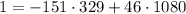
In order to get positive values for u and v, we modify this solution:
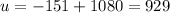 and
and
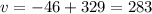
The equation
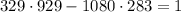
provides the key to solving the original problem.
3. Compute
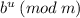 by successive squaring. The value obtained gives the solution x.
by successive squaring. The value obtained gives the solution x.
We have
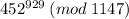 , so
, so
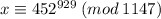
To use this method start by looking at the exponent 929 and represent it as a sum of powers of 2 this is called the binary expansion of 929. To do this, find the largest power of 2 less than your exponent in this case it’s
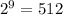 . Subtract 512 from 929 getting 417. And continue in this manner to get:
. Subtract 512 from 929 getting 417. And continue in this manner to get:
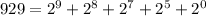
Now
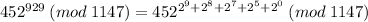
So all you have to do is to calculate the numbers
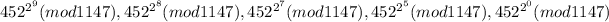
and multiply them together, then take the product