Question

Use a proof by contradiction to prove that the sum of two odd integers is even.

Answer 1

Explanation:

to prove that the sum of two odd integers is even.

Let a and b be two odd integers.

If possible assume that

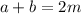`a+b = 2m`, i.e. sum is a product of 2, hence even.

Since a is odd,

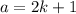`a=2k+1\\` for some integer k.

Subtract a from a+b to get

`b = 2m+1-(2k+1)\\= 2m-2k\\=2(m-k)\\=2l`

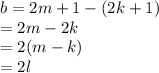
i.e. b is a multiple of some integer l by 2

i.e. b is even.

This contradicts our assumption that both a and b are odd

Hence proved that the sum of two odd integers is even.