Question

Let F be a field, and suppose a EF, a *0. Prove that a has a unique multiplicative inverse.

Answer 1

Answer with Step-by-step explanation:

Let F be a field .Suppose
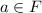`a\in F` and
`a\\eq 0`

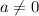
We have to prove that a has unique multiplicative inverse.

Suppose a has two inverses b and c

Then,
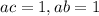`ac=1,ab=1` where 1 =Multiplicative identity

`ac=ab`

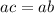
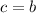`c=b` (cancel a on both sides)

Hence, a has unique multiplicative inverse.