Answer:
Equation of the line is y = -x + 4
Explanation:
When the two lines having their slopes
 and
and
 are perpendicular to each other then
are perpendicular to each other then
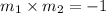
If
 is the slope of the line passing through two points (0, 3) and (4, 7) then
is the slope of the line passing through two points (0, 3) and (4, 7) then
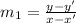
=
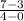
= 1
Now slope of the second line perpendicular to first line will be
 =
=
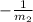
 = -1
= -1
Slope intercept form of the equation of a line is represented by
y = mx + c
where m = slope
c = y intercept
Since the line is passing through (-1, 3) and slope = -1, therefore,
3 = -1 + c
c = 4
Now we plug in these values in the equation.
y = -x + 4
Equation of the line is y = -x + 4