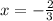Question

Y = –8 – 4x – 3x2Write the equation of the axis of symmetry.


y = –8 – 4x – 3x2

Answer 1

`x=-(2)/(3)`

Explanation:

Given its parameters, we know that this quadratic equation represents a parabola with arms pointing down, and with a maximum value at the point of its vertex.

The equation of its axis of symmetry will be a vertical line that goes through that vertex.

Recall that vertical lines have the form:
`x=number`.

It is essential then that we find the x coordinate of such vertex to complete the general equation form of this vertical axis.

We use the definition for the x value of the vertex of a parabola of the form:

`y=ax^2+bx+c\\x_(vertex) = -(b)/(2a)`

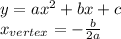
In our case where
`a=-3,\\b=-4,\\c=-8`

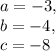
the x-value of the vertex becomes:

`x_(vertex) = -(b)/(2a)=-(-4)/(2(-3)) = (4)/(-6) =-(2)/(3)`

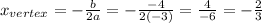
Therefore, the equation for the axis of symmetry of the parabola is:

`x=-(2)/(3)`