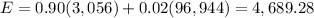Question

Football subscription. In a community of 100,000 students, subscribers to a season ticket for football games tend to renew their subscription with probability 90% and persons presently not subscribing will subscribe for the next season with probability 2%. If the present number of subscribers is 1200, how many subscribers will there be next season and the season following that? (Define all mathematical terms/quantities used.)

Answer 1

i dont know

Explanation:

Answer 2

Next season: 3,056 subscribers.

The season after that: 4,689.28 subscribers

Explanation:

There are 100,000 students in the community, of which 1,200 currently are season ticket subscribers. This means that 100,000 - 1,200 = 98,800 of the students are not season ticket subscribers.

The problem states that current subscribers tend to renew their subscription with probability 90% and persons presently not subscribing will subscribe for the next season with probability 2%.

For next season.

There are currently 1,200 subscribers. 90% of them are expected to renew. There are 98,800 non-subscribers. 2% are expected to subscribe. The expected number of subscribers is:

`E = 0.90(1,200) + 0.02(98,800) = 3,056`

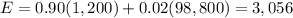
For next season, there are expected to be 3,056 subscribers, and 100,000 - 3,056 = 96,944 non subscribers.

For the season after that:

There are currently 3,056 subscribers. 90% of them are expected to renew. There are 96,944 non-subscribers. 2% are expected to subscribe. The expected number of subscribers is:

`E = 0.90(3,056) + 0.02(96,944) = 4,689.28`