Answer and explanation:
Statement - If the difference of two numbers is even then so is their sum.
Let the two even numbers be '2m' and '2n' with m and n are integers.
The difference of two number is

Now, The sum of the numbers is
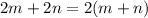
Let
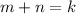 where k is an integer
where k is an integer
Then,
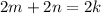 which is also an even number as 2 is multiplied with it.
which is also an even number as 2 is multiplied with it.
So, If the difference of two numbers is even then so is their sum.
For example -
Let two even number 2 and 4.
The difference is
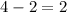 , 2 is even.
, 2 is even.
The sum is
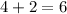 , 6 is even.
, 6 is even.