Question

The monthly profit from the sale of a product is given by P = 36x -0.2x2 - 100 dollars. (a) What level of production maximizes profit? units (b) What is the maximum possible profit?

Answer 1

The level of production that maximizes the profit is 90 units.

The maximum possible profit is 1520 dollars

Explanation:

The profit is modeled by a quadratic equation, thus we can find its vertex x coordinate and we will find the number of units that maximizes the profit using the vertex formula

`x=-\cfrac {b}{2a}`

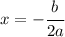
For

`P(x) = ax^2+bx+c`

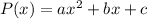
Then we can find the profit just replacing the number of units on the profit equation.

a) What level of production maximizes profit?

We can first write the profit equation in descending order.

`P(x) =-0.2x^2+36x-100`

Thus we get for the coefficients a = -0.2 and b = 36.

Replacing them on the vertex formula

`x=-\cfrac{b}{2a}`

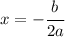
We get

`x=-\cfrac{36}{2(-0.2)}`

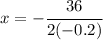
Simplifying we get

`\boxed{x=90\, units}`

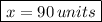
The level of production that maximizes the profit is 90 units

b) What is the maximum possible profit?

We can replace the vertex x coordinate on the profit function, which is finding the value of the profit P(x) for x = 90 units.

`P(90)=-0.2(90)^2+36(90)-100`

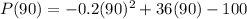
Simplifying we get

`\boxed{P(90) = \$\, 1520}`

The maximum possible profit is 1520 dollars