Answer:
You can proceed as follows:
Explanation:
First solve the quadratic inequality
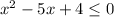 . To do that, factorize, then we have that
. To do that, factorize, then we have that
 . This implies that
. This implies that
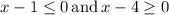
or
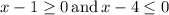
In the first case the solution is the empty set
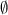 . In the second case the solution is the interval
. In the second case the solution is the interval
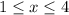 . Now we have that
. Now we have that
![A=[1,4]](https://img.qammunity.org/2020/formulas/mathematics/college/601bize9petrg8iagagcs5960p6eub8o1v.png)
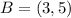
![C=(3,4]](https://img.qammunity.org/2020/formulas/mathematics/college/6ek86vw14phln928xhzldjqnt59zol275p.png) .
.
To show that
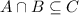 consider
consider
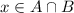 . Then
. Then
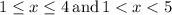 , this implies that
, this implies that
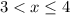 , then
, then
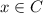 . Now, to show that
. Now, to show that
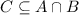 consider
consider
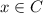 , then
, then
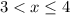 , then
, then
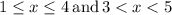 , then
, then
![x\in [1,4] \, \text{and}\, x\in (3,5)](https://img.qammunity.org/2020/formulas/mathematics/college/yaymob7ujw534jueeky6ht2hsd9wz2j1uy.png) , this implies that
, this implies that
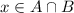 .
.
Observe the image below.