Answer:
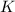 is equidistant from
is equidistant from
 and
and
 .
.
Explanation:
Given that the point
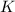 which is on the perpendicular bisector of the line segment having endpoints at
which is on the perpendicular bisector of the line segment having endpoints at
 and
and
 .
.
The given situation can be represented as the diagram as attached in the answer area.
Referring to the
 :
:
 (As it is the perpendicular bisector)
(As it is the perpendicular bisector)
 (As it is the perpendicular bisector)
(As it is the perpendicular bisector)
Also, the side
 is the common side.
is the common side.
Therefore by
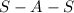 congruence,
congruence,
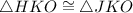
As per the properties of congruent triangles:
Side
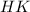 = Side
= Side
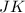
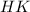 and
and
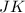 are nothing but the distance of the point
are nothing but the distance of the point
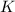 from the end points
from the end points
 and
and
 which are proved to be equal to each other.
which are proved to be equal to each other.
Therefore, we can conclude that:
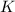 is equidistant from
is equidistant from
 and
and
 .
.