Question

Determine which of the following functions g : Z - Z are permutations of Z (a) g is defined by g(a) = -a + 2 (b) g is defined by g(a) = a^3.

Answer 1

(a) It is a permutation of Z

(b) It is not a permutation of Z

Explanation:

Recall that a permutation of a set S, is just a function g:S--->S which is both injective and surjective. That is to say, g is bijection from S onto S.

(a)

Let's show that g is injective, to do this, we need to show

`g(a)\\eq  g(b)\Rightarrow a \\eq b`

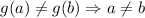
But

`g(a)\\eq  g(b)\Rightarrow -a+2\\eq -b+2 \Rightarrow -a\\eq -b \Rightarrow a\\eq b`

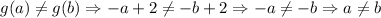
So g is injective.

To prove g is surjective, let's take any integer b and show that there exists an integer a such that g(a) = b.

If we take the integer a = 2-b, then

g(a) = g(2-b) = -(2-b)+2 = -2 +b +2 = b.

So g is also surjective, and thus, a permutation of the integers.

(b)

Although g is injective, g fails to be surjective. To show this, let's show that there is no integer a such that g(a) = 2.

`g(a)=2\Rightarrow a^3=2\Rightarrow a=\sqrt[3]{2}`

but a is not an integer, and g is not surjective. So it is not a permutation.