Question

For the sequence given recursively by ak = 2ak-1 - 3 for k > 2, where a1 = 4, someone has guessed a closed form and used the predicate R(n) for the statement "an = 2^n-1 +3." an = 23. ORO S (a) Are R(1), R(2), R(3), and R(4) true?

Answer 1

True

Explanation:

Given that recurrence formula is

`a_k = 2a_(k-1) -3\\,k>2\\` and

`a_1 =4`

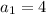
From this we can find

`a_2 = 2a_1-3\\= 8-3 =5\\a_3 =2(5)-3 =7\\a_4 = 2(7)-3 = 11\\`

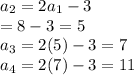
Let us check now R's for these numbers

R(1) is trivially true

`R(2) = 2^(2-1) +3 =5\\R(3) = 2^(3-1) +3 =7\\R(4) = 2^(4-1) +3 =11`

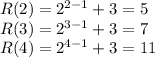
We find that these matches with a values we found using recurrence formula

Hence we can say that R(1), R(2), R(3), and R(4) are true