Question

A credit card company charges 18.6% percent per year interest. Compute the effective annual rate if they compound, (a) annualy, (b) monthly (c) daily and (d) continuosuly.

Answer 1

a) Effective annual rate: 18.6%

b) Effective annual rate: 20.27%

c) Effective annual rate: 20.43%

d) Effective annual rate: 20.44%

Explanation:

The effective annual interest rate, if it is not compounded continuously, is given by the formula

`I=C(1+(r)/(n))^(nt)-C`

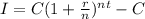
where

C = Amount of the credit granted

r = nominal interest per year

n = compounding frequency

t = the length of time the interest is applied. In this case, 1 year.

In the special case the interest rate is compounded continuously, the interest is given by

`I=Ce^(rt)-C`

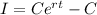
(a) Annually

`I=C(1+(0.186)/(1))-C=C(1.186)-C=C(1.186-1)=C(0.186)`

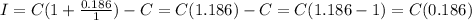
The effective annual rate is 18.6%

(b) Monthly

There are 12 months in a year

`I=C(1+(0.186)/(12))^(12)-C=C(1.2027)-C=C(0.2027)`

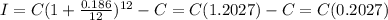
The effective annual rate is 20.27%

(c) Daily

There are 365 days in a year

`I=C(1+(0.186)/(365))^(365)-C=C(1.2043)-C=C(0.2043)`

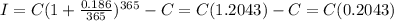
The effective annual rate is 20.43%

(d) Continuously

`I=Ce^(0.186)-C=C(1.2044)-C=C(0.2044)`

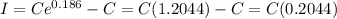
The effective annual rate is 20.44%