Question

For every prime p > 3, 12|(p2 − 1).

Answer 1

Proved

Explanation:

To prove that for every prime p>3 12 divides
`p^2-1`

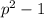
Proof:

Consider
`p^2-1=(p+1)(p-1)`

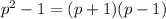
Since p is prime p cannot be even. When p is odd, we have p+1 and p-1 as even number.

This gives us the both p+1 and p-1 are divisible by 2, hence product is divisible by 4

To prove the term is divisible by 3:

We have p-1,p, p+1 as consecutive integers hence any one must be divisible by 3. Since p is prime only either p-1 or p+1 is divisible by3

Hence we have product is divisible by 3 and 4

i.e. 12 divides
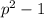`p^2-1`, for all prime p >3