Answer:
As this question is incomplete, but we will try to solve this question by adding our own data to understand the concept of the problem.
Explanation is given below
Explanation:
As this question is incomplete, but we will try to solve this question by adding our own data to understand the concept of the problem.
In order to answer this question we need to have the dimensions of the box.
Let's suppose there are 6 outside surfaces of the box and are equal in dimension including the bottom side which Jan wants to varnish.
So,
Let's suppose,
Surface area of the cube = 6
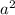
Here, Surface area = 275 square inch
Surface area of the cube = 6
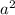 = 275 square inch
= 275 square inch
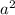 = 275/6 = 45.833
= 275/6 = 45.833
a =
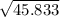
a = 6.77 inches
Now, for the amount of the varnish, we need the spreading rate of the varnish to be used on the box,
Let's suppose it is = 11 square incher per litre.
So,
Required Varnish = Surface area / Spreading rate
Required varnish = 275 / 11
Required varnish = 25 liters
If the 1 container of varnish contains 25 liters then it will be sufficient to protest the outside surfaces of the box.