Question

Your goal is to create a college fund for your child. Suppose you find a fund that offers an APR of 4 %. How much should you deposit monthly to accumulate ​$80, 000 in 18 ​years?

Answer 1

$701.12

Explanation:

Before doing the computing, notice that if we increase an amount D in,say, r%, it means that the new amount obtained is D+r% of D = D+(r/100)D = D(1+r/100).

That is to say, increasing an amount D in r% is equivalent to multiplying it by (1+r/100)

Taking into account that APR stands for Annual Percentage Rate, the amount we deposit will be increased 4% each year.

Generally, in this kind of loans the percentage is prorated monthly. That is to say, the money you have in the account will be increased in (4/12)%= 0.3333% each month.

Let D be the amount we are going to deposit each month.

After the month 1 we will have the money increased in 0.3333% plus the new deposit

`D(1+(0.3333)/(100))+D=D(1+1.0033)`

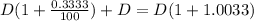
After the month 2 we will have the money we already had increased in 0.3333% plus the new deposit D

`D(1+1.0033)(1.0033)+D=D(1.0033+1.0033^2)+D=D(1+1.0033+1.0033^2)`

After the month 3 we will have, for the same reason,

`D(1+1.0033+1.0033^2+1.0033^3)`

It can be noticed then, that after 18 years (96 moths) we will have an amount in the fund of

`D(1+1.0033+1.0033^2+...+1.0033^(96))`

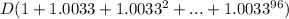
If we call

`S=1+1.0033+1.0033^2+...+1.0033^(96)`

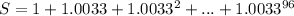
then

`1.0033S=1.0033+1.0033^2+...+1.0033^(96)+1.0033^(97)`

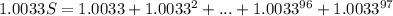
Subtracting the equations

`S-1.0033S=1-1.0033^(97)\Rightarrow S(1-1.0033)=1-1.0033^(97)`

and we have

`S=(1-1.0033^(97))/(1-1.0033)=114.10298`

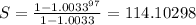
So, after 18 years the amount in the fund will be

114.10298D

If we want this amount to be $80,000 then 114.10298D=80,000

`D=(80,000)/(114.10298)\approx \$ 701.12`

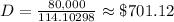
So, the money we would have to deposit each month in a fund with an APR of 4% to accumulate $80,000 in 18 years, is

`\boxed{D=\$701.12}`