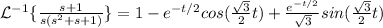Question

B-2-11. Find the inverse Laplace transform of s + 1/s(s^2 + s +1)

Answer 1

`\mathcal{L}^(-1)\{(s+1)/(s(s^(2) + s +1))\}=1-e^(-t/2)cos((√(3) )/(2)t )+(e^(-t/2))/(√(3) )sin((√(3) )/(2)t)`

Explanation:

let's start by separating the fraction into two new smaller fractions

.

First, s(s^2+s+1) must be factorized the most, and it is already. Every factor will become the denominator of a new fraction.

`(s+1)/(s(s^(2) + s +1))=(A)/(s)+(Bs+C)/(s^(2)+s+1)`

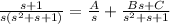
Where A, B and C are unknown constants. The numerator of s is a constant A, because s is linear, the numerator of s^2+s+1 is a linear expression Bs+C because s^2+s+1 is a quadratic expression.

Multiply both sides by the complete denominator:

`[{s(s^(2) + s +1)](s+1)/(s(s^(2) + s +1))=[(A)/(s)+(Bs+C)/(s^(2)+s+1)][{s(s^(2) + s +1)]`

Simplify, reorganize and compare every coefficient both sides:

`s+1=A(s^2 + s +1)+(Bs+C)(s)\\\\s+1=As^(2)+As+A+Bs^(2)+Cs\\\\0s^(2)+1s^(1)+1s^(0)=(A+B)s^(2)+(A+C)s^(1)+As^(0)\\\\0=A+B\\1=A+C\\1=A`

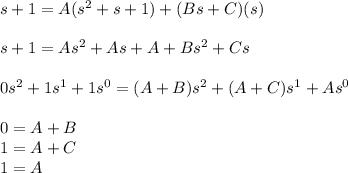
Solving the system, we find A=1, B=-1, C=0. Now:

`(s+1)/(s(s^(2) + s +1))=(1)/(s)+(-1s+0)/(s^(2)+s+1)=(1)/(s)-(s)/(s^(2)+s+1)`

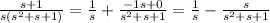
Then, we can solve the inverse Laplace transform with simplified expressions:

`\mathcal{L}^(-1)\{(s+1)/(s(s^(2) + s +1))\}=\mathcal{L}^(-1)\{(1)/(s)-(s)/(s^(2)+s+1)\}=\mathcal{L}^(-1)\{(1)/(s)\}-\mathcal{L}^(-1)\{(s)/(s^(2)+s+1)\}`

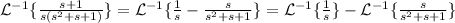
The first inverse Laplace transform has the formula:

`\mathcal{L}^(-1)\{(A)/(s)\}=A\\ \\\mathcal{L}^(-1)\{(1)/(s)\}=1\\`

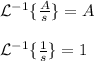
For:

`\mathcal{L}^(-1)\{-(s)/(s^(2)+s+1)\}`

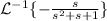
We have the formulas:

`\mathcal{L}^(-1)\{(s-a)/((s-a)^(2)+b^(2))\}=e^(at)cos(bt)\\\\\mathcal{L}^(-1)\{(b)/((s-a)^(2)+b^(2))\}=e^(at)sin(bt)`

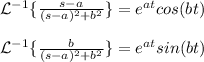
We have to factorize the denominator:

`-(s)/(s^(2)+s+1)=-(s+1/2-1/2)/((s+1/2)^(2)+3/4)=-(s+1/2)/((s+1/2)^(2)+3/4)+(1/2)/((s+1/2)^(2)+3/4)`

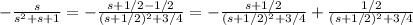
It means that:

`\mathcal{L}^(-1)\{-(s)/(s^(2)+s+1)\}=\mathcal{L}^(-1)\{-(s+1/2)/((s+1/2)^(2)+3/4)+(1/2)/((s+1/2)^(2)+3/4)\}`

`\mathcal{L}^(-1)\{-(s+1/2)/((s+1/2)^(2)+3/4)\}+\mathcal{L}^(-1)\{(1/2)/((s+1/2)^(2)+3/4)\}\\\\\mathcal{L}^(-1)\{-(s+1/2)/((s+1/2)^(2)+3/4)\}+(1)/(2) \mathcal{L}^(-1)\{(1)/((s+1/2)^(2)+3/4)\}`

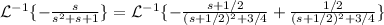
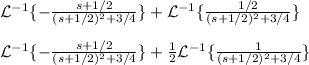
So a=-1/2 and b=(√3)/2. Then:

`\mathcal{L}^(-1)\{-(s+1/2)/((s+1/2)^(2)+3/4)\}=e^{-(t)/(2)}[cos(√(3)t )/(2)]\\\\\\(1)/(2)[(2)/(√(3) ) ]\mathcal{L}^(-1)\{(√(3)/2 )/((s+1/2)^(2)+3/4)\}=(1)/(√(3) ) e^{-(t)/(2)}[sin(√(3)t )/(2)]`

Finally:

`\mathcal{L}^(-1)\{(s+1)/(s(s^(2) + s +1))\}=1-e^(-t/2)cos((√(3) )/(2)t )+(e^(-t/2))/(√(3) )sin((√(3) )/(2)t)`