Question

Find the Parametric equation of the line, which passes through the points: a=(1,2,3), b=(2,0,-4)

Answer 1

(x,y,z) = (1+s, 2-2s,3-7s)

Explanation:

Given that a line in three dimension passes through two points a and b

We have equation of the line passing through two points

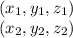`(x_1,y_1,z_1) \\(x_2,y_2,z_2)` is

`(x-x_1)/(x_2-x_1) =(y-y_1)/(y_2-y_1) =(z-z_1)/(z_2-z_1)`

Substitute for the two points and equate to s

`(x-1)/(2-1) =(y-2)/(0_2) =(z-3)/(-4-3)=s`

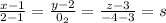
Simplify to write

`(x-1)/(1) =(y-2)/(-2) =(z-3)/(-7) =s\\x=1+s:  y= 2-2s:   z=3-7s`

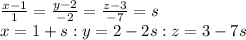
Thus parametric form is

(x,y,z) = (1+s, 2-2s,3-7s)