Answer:
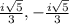
Explanation:
Since this quadratic equation does not contain a term in x, we can proceed to isolate the term with the unknown on the left hand side, by subtracting 10 from both sides, and then dividing both sides by 9 as shown below:
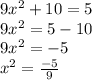
Now we apply the square root on both sides to get the value/s for x that make the equation true. Remember to consider plus and minus signs to take care of the two possible solutions involved in the root, so let's do each case separately:
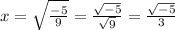
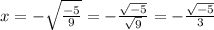
We notice that the numerator on the right side renders the square root of a NEGATIVE number (-5). This originates the imaginary unit "i":
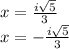
Therefore the correct answer is the third listed option in your pasted image