Answer:
(I) Yes
(II) Yes
(III) No
(IV) No
Explanation:
(I) The relation is a function from A to A as it satisfies both existence and uniqueness: every element of A (domain) is related to only one element of A (codomain).
(II) The relation is an everywhere defined function as every element of A is related to an element of A.
(III) The relation is not an onto (surjective) function.
Let's recall the definition of an onto function:
An onto function f : A -> B satisfies:
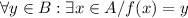 .
.
In this case,
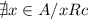 . So, the function is not onto.
. So, the function is not onto.
(IV) The relation is not a one to one (injective) function.
Let's recall the definition of a one to one function:
A one to one function f : A -> B satisfies:
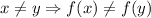 .
.
In this case, both
 and
and
 relate to
relate to
 , so the function is not one to one.
, so the function is not one to one.