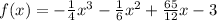Question

Find a polynomial of the form

f(x) = ax3 + bx2 + cx + d

such that f(0) = −3, f(1) = 2, f(3) = 5, and f(4) = 0. (A graphing calculator is recommended.)

Answer 1

`f(x)=-(1)/(4)x^3-(1)/(6)x^2+(65)/(12)x-3`

Explanation:

We are given that

`f(x)=ax^3+bx^2+cx+d`

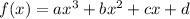
f(0)=-3,f(1)=2,f(3)=5 and f(4)=0

We have to find the polynomial

Substitute the value x=0 then ,we get

f(0)=d=-3

Substitute x=1 then we get

`a+b+c-3=2`

`a+b+c=2+3=5`

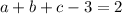
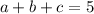`a+b+c=5` (equation I)

Substitute x=3 then we get

`a(3)^3+b(3)^2+c(3)-3=5`

`27a+9b+3c=5+3=8`

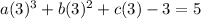
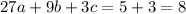
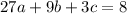`27a+9b+3c=8` (Equation II)

Substitute x=4 then we get

`a(4)^3+b(4)^2+c(4)-3=0`

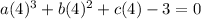
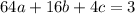`64a+16b+4c=3` (Equation III)

Equation I multiply by 3 then subtract from equation II

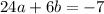`24a+6b=-7` (Equation IV)

Equation II multiply by 4 and equation III multiply by 3 and subtract equation II from III

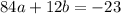`84a+12b=-23` (Equation V)

Equation IV multiply by 2 and then subtract from equation V

`36a=-9`

`a=-(9)/(36)`

`a=-(1)/(4)`

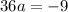
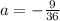
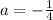
Substitute the value of a in equation IV then we get

`24(-(1)/(4))+6b=-7`

`-6+6b=-7`

`6b=-7+6=-1`

`b=-(1)/(6)`

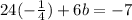
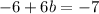
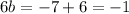
Substitute the value of b in equation I then we get

`-(1)/(4)-(1)/(6)+ c=5`

`-(5)/(12)+c=5`

`c=5+(5)/(12)=(65)/(12)`

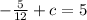
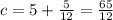
Substitute the values then we get

`f(x)=-(1)/(4)x^3-(1)/(6)x^2+(65)/(12)x-3`