Question

The Industrial Statistics class consists of 50 DCIT students and 40 Engineering students. The probability of a student failing from DCIT and Engineering are, 0.10 and 0.01 respectively. One of the students failed the course. What is the probability that it is a student from DCIT. [10

Answer 1

Answer: 0.9259

Explanation:

Given : The Industrial Statistics class consists of 50 DCIT students and 40 Engineering students.

Total students = 50+40=90

Probability of selecting a DCIT student=
`P(D)=(50)/(90)=(5)/(9)`

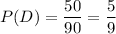
Probability of selecting a Engineering student=
`P(E)=(40)/(90)=(4)/(9)`

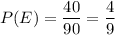
Also, The probability of a student failing from DCIT and Engineering are, P(D|F)=0.10 and P(E|F)=0.01 respectively.

Now, One of the students failed the course. Then by Bayes theorem, the probability that it is a student from DCIT will be :-

`P(F|D)=(P(D)\cdot P(D|F))/(P(D)\cdot P(D|F)+P(E)\cdot P(E|F))\\\\=((5)/(9)*0.10)/((5)/(9)*0.10+(4)/(9)*0.01)\\\\=(0.0555555555556)/(0.06)=0.925925925927\approx0.9259`

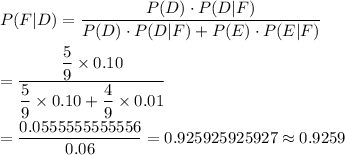
Hence, the probability that it is a student from DCIT = 0.9259