Question

What is the coefficient of x^8 y^2 in the expansion of (x + y)^10?

Answer 1

The coefficient of
`x^(8)y^(2)` is
`45`.

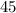Explanation:

By the binomial theorem we have that

`(x+y)^(n)=\sum_(k=0)^(n) {{n}\choose{k}} x^(n-k)y^(k)`.

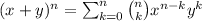where
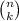`{n \choose k}` is known has a binomial coefficient and it can be compute by
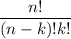`(n!)/((n-k)! k!)`. The symbol
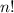`n!` stands for the factorial of
`n`, that is to say,
`n!=1* 2* \cdots * n`

So if you have
`n=10` then we can replace on the expression of the binomial theorem to obtain

`(x+y)^(10)=\sum_(k=0)^(10){10\choose k}x^(10-k)y^(k)`

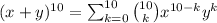
In order to obtain the coefficient of
`x^(8)y^(2)` we find the term where
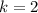`k=2`, that is to say,

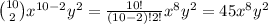`{10\choose 2} x^(10-2)y^(2)=(10!)/((10-2)!2!)x^(8)y^(2)=45x^(8)y^(2)`. We conclude that the coefficient we were looking for is
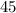`45`.