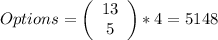Question

A poker hand consists of five cards from a standard 52 card deck with four suits and thirteen values in each suit; the order of the cards in a hand is irrelevant. How many hands consist of 2 cards with one value and 3 cards of another value (a full house)? How many consist of 5 cards from the same suit (a flush)?

Answer 1

There are 3744 possible full house hands in five-cards poker.

There are 5148 possible flush hands in five-cards poker.

Explanation:

For a full house, we have to have 2 out of 4 of the same value with 13 different values, plus 3 out of 4 of the same value with 12 different values (because one was used for the first 2 cards). We can count those different options by using combinatorics (choosing 3 out of 4 and (in probability, and means those two are independent, meaning we multiply the options) 2 out of 4) and multiplying them by the different options of values:

`Options = \left(\begin{array}{ccc}4\\2\end{array}\right)*13 * \left(\begin{array}{ccc}4\\3\end{array}\right)*12=3744`

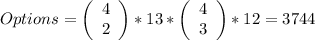
In order to count how many hands result in a flush, we do it the same way, but now, we have to choose 5 out of 13 cards, times 4 possible suits:

`Options = \left(\begin{array}{ccc}13\\5\end{array}\right)*4=5148`