Answer:
The statement
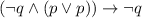 is a tautology
is a tautology
Explanation:
A tautology is a statement that is true for every assignment of truth values to its simple components.
a) A truth table shows how the truth or falsity of a compound statement depends on the truth or falsity of the simple statements from which it's constructed.
We have the statement
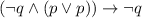 , which is compound by these statements:
, which is compound by these statements:
and we are going to use these simple statements to build the truth table.
The last column contains only true values. Therefore, the statement is a tautology.
b) We are going to use the table of logical equivalences as follows:
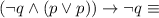
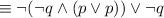 by the logical equivalence involving conditional statement.
by the logical equivalence involving conditional statement.
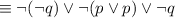 by De Morgan's Law
by De Morgan's Law
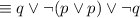 by the Double negation law
by the Double negation law
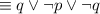 by the Idempotent law
by the Idempotent law
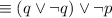 by Associative law
by Associative law
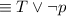 by Negation law
by Negation law
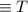 by Domination law
by Domination law