Question

The scores for Engineering students doing Math 2250 in 2018 is as follows: 56, 67, 95, 76, 82, 67, 55, 23, 97, 89, 99, 49 i.) From the 12 scores, the sum of the values () = 855 and the sum of the squared values () = 66725. Use these values to calculate the standard deviation (SD) and the mean. [3] ii.) Determine the mode and the median. [2] iii.) Which of the above three measures (mean, median and mode) is most appropriate for this data and why? [2] iii.) Calculate the Coefficient of Variation (CV) and Interquartile Range (IQR) for this data set. Would you use SD, CV or IQR as a measure of spread for this data? Explain your answer. [3]

Answer 1

i) Mean = 71.25, SD = 22

ii) Mode = 67, Median = 71.5

iii) Mean

iv) SD

Explanation:

i)

The mean is

`\bar x=(\sum values)/(number\;of\;values)=(855)/(12)=71.25`

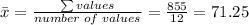
Once you know the mean, the standard deviation s can be obtained through the following formula:

`s=\sqrt{(\sum squared\;values)/(n)-\bar x^2}`

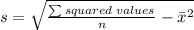
where n is the number of values. So,

s = 21.996 that we can approximate to 22

ii)

Ordering the data in ascending mode

23, 49, 55, 56, 67, 67, 76, 82, 89, 95, 97, 99

The median is the midpoint between 67 and 76.

The mode is 67 (the greatest frequency)

Median = (67+76)/2= 71.5

iii)

The interval [mean-s, mean+s]=[71.25-22, 71.25+22]=[ 49.25, 93.25] contains 7 values of the data

The interval [median-s, median+s]=[71.5-22, 71.5+22]=[49.5, 93.5] contains 7 values of the data

The interval [mode-s, mode+s]=[67-22,67+22]=[45, 89] contains 7 values of the data.

So, for this set of data either the mean or the median could be chosen, but given that the mean is the most used average by far, it is recommended to use the mean.

Iii)

Coefficient of variation CV=(s/mean)*100 = (22/71.25)*100=30.88%

The median of the first 6 data is 55.5

The median of the last 6 data is 92

So the Interquartile Range is 92-55.5 = 36.5

The CV is non dimensional (%) and mostly used to measure the variation of the dispersion around the mean between different sets of data.

The interval [71.25-IQR,71.25+IQR]=[ 34.75, 107.75] contains practically all the data so it would be useless as a dispersion measure.

So the most convenient measure of dispersion, and the most used by far, is the SD.