Question

Use the formula for continuous compounding to compute the balance in the account after 1,5, and 20 years. Also, find the APY for the account A $7000 deposit in an account with an APR of 3.6% The balance in the account after 1 year is approximately $ (Round to the nearest cent as needed.) The balance in the account after 5 years is approximately $ (Round to the nearest cent as needed.) The balance in the account after 20 years is approximately (Round to the nearest cent as needed.) The APY for the account is approximately (Round to two decimal places as needed.) Enter your answer in each of the answer boxes E O Type here to search hp

Answer 1

After 1 year: $7,256.59

After 5 years: $8,380.52

After 20 years: $14,381.03

APY = 3.66%

Explanation:

If you deposit $7000 with an interest of 3.6%, after 1 year using continuous compounding, you will have

`7000e^(0.036)=7,256.59`

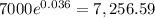
After 5 years you will have

`7000e^(5(0.036))=8,380.52`

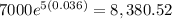
After 20 years

`7000e^(20(0.036))=14,381.03`

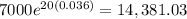
To find the APY for the account, we have to compute the interest earned in one year.

We can do it by cross multiplying or by finding a number x such that

`7000(1+(x)/(100))=7,256.59`

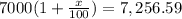
Operating on this equation we obtain

x = 0.0366 or 3.66%